CONOCIMIENTOS PREVIOS
PAR ORDENADO
PRODUCTO CARTESIANO:
Sean A y B conjuntos. Al conjunto formado por todos los pares ordenados de primera componente en A y segunda componente en B, se le denota A x B y se le llama producto cartesiano de A y B. Simbólicamente:
A x B = {(x, y) / x Î A Ù y Î B}.
En consecuencia:
(x, y) Î A x B Û x Î A Ù y Î B
(x, y) Ï A x B Û x Ï A Ú y Ï B
A x B = {(1, 3),(1, 4),(1, 5),(2, 3),(2, 4),(2, 5)}.
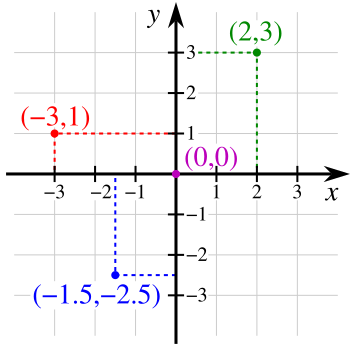
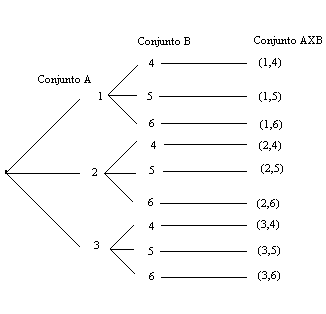
REPRESENTACIÓN GRAFICA DEL PRODUCTO CARTESIANO:

PAR ORDENADO
Un par ordenado es un tupla de dos elementos, tal que uno puede ser distinguido como el primero y el otro como el segundo. Un par ordenado con primer elemento a y con segundo elemento b es escrito usualmente como (a, b). Dos pares ordenados cumplen:
No es lo mismo (a,b) que (b,a) en otras palabras (a,b) es diferente de (b,a).(a, b) = (c, d) si y sólo si a = c y b = d
PRODUCTO CARTESIANO:
Sean A y B conjuntos. Al conjunto formado por todos los pares ordenados de primera componente en A y segunda componente en B, se le denota A x B y se le llama producto cartesiano de A y B. Simbólicamente:
En consecuencia:
(x, y) Ï A x B Û x Ï A Ú y Ï B
Ejemplo 1:
Sean A = {1, 2} y B = {3, 4, 5} el producto cartesiano A x B será:
Sean A = {1, 2} y B = {3, 4, 5} el producto cartesiano A x B será:
DIAGRAMA SAGITAL

PLANO CARTESIANO

DIAGRAMA DE ÁRBOL

RELACIONES | ||
| Una relación es un subconjunto del producto cartesiano que cumple con una determinada condición. Las relaciones entre conjuntos forman pares ordenados partiendo de una condición dada. Por ejemplo: Dados los conjuntos: A = {1; 3; 4} y B = {2; 8; 9}; Encontrar un conjunto C, cuyos pares ordenados cumplan con la condición "Doble de" |  | |
| El Conjunto formado por los primeros componentes de cada par de la relación se llama DOMINIO. EL Conjunto formado por los segundos componentes de cada par de la relación se llama CODOMINIO. Si establecemos una relación entre los elementos de un mismo conjunto, existen tres propiedades fundamentales que pueden cumplirse en esa relación; propiedades: reflexiva, simétrica y transitiva. | ||
Propiedad Reflexiva | ||
Se refiere a que todos los elementos de un conjunto tienen relación consigo mismo. Se representa a R a. | ||
Propiedad Simétrica | ||
Si un elemento del primer conjunto se relaciona con un elemento del segundo conjunto, este a su vez se relaciona con el elemento del primer conjunto. | ||
Propiedad Transitiva | ||
Un elemento de un conjunto se relaciona con otro y este a su vez con un tercero, por tanto el primer elemento mantiene relación con el tercero. | ||
Relación de orden | ||
| Es aquella en que los elementos pueden ordenarse y cumple con las propiedades reflexiva y simétrica. Ejemplo: Dado el conjunto A = {1, 2, 3}, y la relación de orden "Mayor que"; a) reflexiva, b) simétrica y; c) transitiva. a) Propiedad reflexiva: 1 no es mayor que 1 b) Propiedad simétrica: 2 es mayor que 1 1 no es mayor que 2 c) Propiedad Transitiva 3 es mayor que 2 2 es mayor que 1 Por tanto 3 es mayor que 1 | ||
Relación de equivalencia | ||
Es la relación que cumple con las tres propiedades: Reflexiva, Simétrica y Transitiva. Ejemplo: Dada la relación "Ser igual" Propiedad Reflexiva: a = a Propiedad Simétrica: Si a = b, entonces b = a Popiedad Transitiva: Si a = b y b = c, entonces a = c CONCEPTO DE FUNCIÓN: Una función puede considerarse como un caso particular de una relación o de correspondencia matemática. Cada relación o correspondencia de un elemento  con un (y sólo un) con un (y sólo un)  se denota se denota  , en lugar de , en lugar de 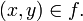 Formalmente, pedimos que se cumplan las siguientes dos condiciones:
Ejemplo
| ||

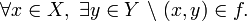

 , tiene como dominio, codominio e imagen a todos los
, tiene como dominio, codominio e imagen a todos los 

 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +
, sólo tendrá como imagen los valores comprendidos entre 0 y + , con
, con
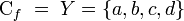


Gracias!
ResponderEliminarok... seño muchas gracias me quedo claro o bueno eso digo
ResponderEliminar